En este artículo vamos a realizar un caso práctico sencillo sobre como calcular el índice o coeficiente de Gini el cual nos indica la desigualdad que vamos a tener en la distribución de la renta en una población.
Para comenzar vamos a crear un cuadro con los conceptos estadísticos más importantes para que sepamos en todo momento calcularlos e interpretarlos.
xi: Vamos a utilizarlo como el salario de referencia que cobra cada persona de nuestra muestra.
ni: Número de personas que cobran el salario especificado anteriormente.
N: Número total de observaciones o personas Σni.
Ni: Número acumulado de personas, se realiza por la suma simple del elemento anterior.
Pi: Proporción acumulada de gente que cobra el salario su fórmula -> Pi = Ni / N *100
mi: Monto total de salario por población, si fórmula es la siguiente -> mi = xi*ni.
Mi: Salario acumulado por población.
M: Total de los salarios en la economía.
Qi: % que cobra cada población con relación al total de la economía -> Qi = Mi / M *100
G: O índice de Gini, su fórmula es G = ((ΣPi*Qi+1) – (ΣPi+1*Qi)) / 10.000
Estas son todas las nomenclaturas y fórmulas que vamos a necesitar para realizar el coeficiente o índice de Gini.
Ejemplo práctico resuelto sobre como calcular el índice de Gini
Sabemos que una economía está compuesta por 1.000 personas, cuya distribución salarial mensual es la siguiente.
583 personas cobran un salario de 1.150€, 237 cobran un salario de 1.985€, 149 cobran 2487€ y 31 personas cobran 3.175€.
Con los datos especificados anteriormente, calcular el índice de Gini.
Resolución del ejercicio práctico para calcular el índice de Gini
El primer paso es ordenar los datos en una tabla de doble entrada, nuestro enunciado ya nos ha dado el valor de N = 1.000 personas, y nos ha dado los valores de xi (salarios) así como el número de personas que cobran ese salario (ni). Por lo tanto si organizamos la siguiente tabla quedaría así:
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | |||||||
| 1.985 | 237 | |||||||
| 2.487 | 149 | |||||||
| 3.175 | 31 | |||||||
| Σni = N = 1.000 |
Con los datos del enunciado hemos construido la primera tabla que iremos completando a lo largo de la resolución del ejercicio.
Completando la columna de Ni, que, sabemos que representa la población acumulada en cada escalón la tabla quedaría de la siguiente forma:
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | ||||||
| 1.985 | 237 | 820 (583+237) | ||||||
| 2.487 | 149 | 969 (820+149) | ||||||
| 3.175 | 31 | 1.000 (969+31) | ||||||
| Σni = N = 1.000 |
Una vez tenemos los datos de frecuencia acumulada procedemos a realizar la columna que representa la proporción acumulada que cobra el salario especificado. Esta se realiza con la siguiente fórmula :
Pi = Ni / N *100
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | 58,3 | |||||
| 1.985 | 237 | 820 | 82 | |||||
| 2.487 | 149 | 969 | 96,9 | |||||
| 3.175 | 31 | 1.000 | 100% | |||||
| Σni = N = 1.000 |
Con los datos de esta tabla ya podemos sacar las primeras interpretaciones. Por ejemplo, podemos decir que el 82% de la población cobra un salario igual o menor a 1.985€/mes. O que el 58,3% de la población cobra un salario de 1.150€/mes
Continuando ahora con el monto total de salarios, es decir la cantidad total de salarios pagados en cada escalón representado por mi cuya fórmula es xi*ni
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | 58,3 | 670.450 (1.150*583) | ||||
| 1.985 | 237 | 820 | 82 | 470.445 (1.985*237) | ||||
| 2.487 | 149 | 969 | 96,9 | 370.563 (149*2.487) | ||||
| 3.175 | 31 | 1.000 | 100% | 98.425 (3.175*31) | ||||
| Σni = N = 1.000 | Σmi = M = 1.609.883 |
Con esta información podemos asegurar que en la economía descrita se paga un total de 1.609.883€ de salarios todos los meses.
Ahora vamos a calcular los salarios acumulados de la economía, representados por Mi cuya ecuación es igual a la de Ni por lo que omitiremos los cálculos.
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | 58,3 | 670.450 | 670.450 | |||
| 1.985 | 237 | 820 | 82 | 470.445 | 1.140.895 | |||
| 2.487 | 149 | 969 | 96,9 | 370.563 | 1.511.458 | |||
| 3.175 | 31 | 1.000 | 100% | 98.425 | 1.609.883 | |||
| Σni =1.000 | Σmi = 1.609.883 |
Una vez hemos calculado el monto total por poblaciones calculamos la distribución de Qi que nos indica que porcentaje del salario cobra cada población en relación con el salario total de la economía. Su formula es la siguiente: Qi = Mi / M *100
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | 58,3 | 670.450 | 670.450 | 41,65 | ||
| 1.985 | 237 | 820 | 82 | 470.445 | 1.140.895 | 70,87 | ||
| 2.487 | 149 | 969 | 96,9 | 370.563 | 1.511.458 | 93,89 | ||
| 3.175 | 31 | 1.000 | 100% | 98.425 | 1.609.883 | 100% | ||
| Σni =1.000 | Σmi = 1.609.883 |
Una vez hemos realizado Qi podemos realizar las siguientes afirmaciones. Las personas que cobran 1.150€ representan el 41,65% de los salarios totales pagados en la economía. Así como que las personas que cobran 2.487€ o menos representan el 93,89% de los salarios totales pagados en la economía.
En este último paso con nuestra tabla realizamos los cálculos que nos indica la tabla, donde Pi+1*Qi sería por ejemplo 82%*41,65%
| xi (salarios) | ni (personas) | Ni | Pi | mi | Mi | Qi | Pi+1*Qi | Pi*Qi+1 |
| 1.150 | 583 | 583 | 58,3 | 670.450 | 670.450 | 41,65 | 3.415,3 | 4131,72 |
| 1.985 | 237 | 820 | 82 | 470.445 | 1.140.895 | 70,87 | 6.867,30 | 7.698,98 |
| 2.487 | 149 | 969 | 96,9 | 370.563 | 1.511.458 | 93,89 | 9.389 | 9.690 |
| 3.175 | 31 | 1.000 | 100% | 98.425 | 1.609.883 | 100% | ||
| Σni =1.000 | Σmi = 1.609.883 | Σ=19.671,6 | Σ=21.520,7 |
Una vez hemos realizado todos los cálculos y hemos obtenido que ΣPi+1*Qi = 19.671,6 y que ΣPi*Qi+1 = 21.520,7 solo nos queda aplicar la fórmula de Gini que es la siguiente
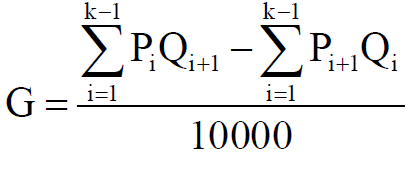
Por lo que finalmente sabemos que el índice de Gini o coeficiente de Gini es G = (21.520,7 – 19.671,6) / 10.000 -> G = 0,18491
Conclusiones e interpretación del índice de Gini
Como sabemos el índice de Gini tiene la siguiente interpretación:
G = 1 se corresponde con la perfecta desigualdad (una persona tiene todos los ingresos y los demás ninguno)
G = 0 se corresponde con la perfecta igualdad (todos tienen los mismos ingresos)
En este caso vemos que los saltos entre ingresos no son muy abultados y entre la persona que menos cobra y la que más cobra existe una diferencia de 2.025€. Además como se puede comprobar el grueso de la población está cobrando el salario mínimo de la economía y su salario seguido del que se diferencia en poco más de 800€.
Por lo tanto podemos dictaminar que el resultado se corresponde con la distribución estimada de los ingresos en la población.